My final forms evolved from a simple spiral. Unsure where I was going with my theme of logarithmic spirals, I watched 'Generating a Spiral in Rhino’s Grasshopper Plugin' tutorial on Designalyze. I was shown this tutorial from my tutor Melody. This is the basis of all my iterations.
To watch this tutorial please click on the link below:
http://www.designalyze.com/?p=3
The rest of the components of my definition were added by experimentation with grasshopper. However i did receive assistance from my classmate Rose with the relocating scaled instances of the form to different points on my spiral.
Wednesday, March 30, 2011
Tuesday, March 29, 2011
Sunday, March 27, 2011
Final Renders - 2nd Evolution of Inital iterations
My Third set of iterations investigated the geometric progression of the spiral, the increasing scale. I still maintain the basic principle of the spiral; however instead of representing my theme with the use of surfaces connected by curves, I used spheres which I programmed to increase in size as the rise in height with the use of a series node. Then with the image of a vegetable in my head, I wanted to represent the small logarithmic spirals within the large spiral. With the use of vector, move and scale formula within my flow graph to create what I felt to be an sophisticated & graceful system.
Final Renders - Evolution of iterations
My second set of iterations evolved from the first set, but this time I added an additional graph that controlled the height of these organic spirals, shown in the images above. The XY points were still controlled by the one value, but the Z points were now affected by an additional formula. I found that when the z points were controlled completely separate of the XY Values much more interesting forms were created.
Final Renders - Initial Iterations
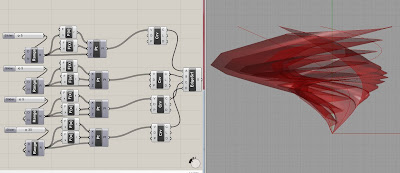
My initial sets of iterations evolved from the use of a flow graph that formed a spiral; from this I added four extra spirals that all had different XY values attached to a curves joined by an edge surface, consequently forming a shape characteristic of a hurricane. As I reduced the range it formed a more elegant shape. Joining the edge surface directly from the points created a much more mechanical form, reminiscent of the sectional lines in a nautilus shell.
Saturday, March 26, 2011
Draft Poster
Background - I custom made this background using a range of formulas that relate to the fibonnaci sequence. Image Boxes - My idea with the images boxes is to distribute the sets of four iterations into their three main groups. I want to make the background translucent with approximately 60% opacity. with the renders organised accordingly.
Colour Choices - My background is black with white text to represent a blackboard riddled with formulas. As I am focusing on the theme of Logarithmic spirals found in nature I have decided to render my objects in a shallow ocean blue. I would like to keep my text black so i does not take away from the intensity of my renders.
Body Text & Title Box - I would like to keep the same theme running with a translucent background, however this time with approximately 75% opacity So the background does not interfere with my Text. I will have to experiment with this and see what is appropriate.
Friday, March 25, 2011
Thursday, March 24, 2011
Experiment 7 - ACCIDENTAL modelling
1 of my 3 initial images was of this snake. I was very interested in the texture of the snakes skin, and all its aesthetic qualities. I choose to focus on logamarithmic spirals instead, however, I was interested to discover that these too concepts are not too different after all. Whilst experimenting with the spheres attached to the points of my spiral i came across this rather scale like creation. The spheres weren't scaled as they were in the last experiment, however when the value controlling the amount of points and subsequently spheres that were created was significantly increased, the spheres overlapped and it was accidently created.
Experiment 4, 5 & 6 - Expansion on Spirals
My theme is logamarithmic spirals. I have been experimenting with a few different consepts stemming from them same intial idea.
This shape similarly started off with the initial spirals, but this time did not use a curve attatched to my points. I then wanted to lay a series of planes on the different points. I found that i had to use a 4pt surface to create the effect i wanted; planes that were shaped depending on their orientation on the spiral.
This experiement deals with spheres. I ws experimenting with scaling according to there XYZ location. For this i plugged series in the radius of the sphere, which was plugged into the points on the spiral. I initially came across the problem that i could only manually enter a series of numbers, but wanted to create a series that could be easily adjusted. After i solved this issue, i came across a problem that was creating the spheres to scale to a certin point and then stop increasing in size. I realised that the slider plugged into the C value of series(controlling the amount of spheres created) had to be the same as the slider plugged into the N value of the range(controlling the amount of points in the spiral).
This model was created using a series of spirals created using curves attatched to points. I then experimented with creating an edge surface between the different spirals.
This shape similarly started off with the initial spirals, but this time did not use a curve attatched to my points. I then wanted to lay a series of planes on the different points. I found that i had to use a 4pt surface to create the effect i wanted; planes that were shaped depending on their orientation on the spiral.
This experiement deals with spheres. I ws experimenting with scaling according to there XYZ location. For this i plugged series in the radius of the sphere, which was plugged into the points on the spiral. I initially came across the problem that i could only manually enter a series of numbers, but wanted to create a series that could be easily adjusted. After i solved this issue, i came across a problem that was creating the spheres to scale to a certin point and then stop increasing in size. I realised that the slider plugged into the C value of series(controlling the amount of spheres created) had to be the same as the slider plugged into the N value of the range(controlling the amount of points in the spiral).Experiment 3 - More Variations on the spiral
This variation i changed the polyline to a curve connecting to the points of the spiral. It has a very dfferent effect. The curve does not pass through the points of the spiral.
Experiment 1 - Spirals
This first spiral i used a polyline connected through the points of the spiral.
Wednesday, March 9, 2011
Hurricane Isabel
Theme 3 - logarithmic spiral
The biological structure of a nautilus shell is an example of a logarithmic spiral. A logarithmic spiral or growth spiral is a special kind of spiral curve which often appears in nature. The distances between the turnings of a logarithmic spiral increase in geometric progression. Other great examples of logarithmic spirals include the arms of spiral galaxies, the nerves of the cornia and the arms of a tropical cyclone.As Melody has explained to me the nautilus shell can also be described by the fibonacci sequence which is a sequence of numbers in which each number equals the sum of the two preceding numbers.
Subscribe to:
Posts (Atom)